抽时间复习一下数据结构这些基础，呜哇~

线性结构

序

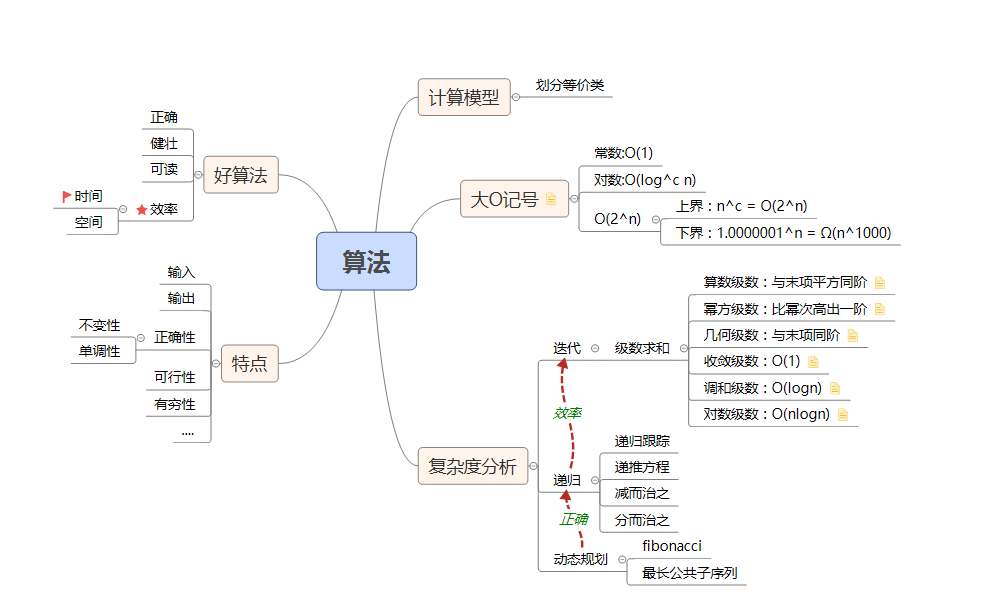
这里面的东西倒是好解，这里只记录下动态规划的两个例子：

fibonacci：生兔砸，走楼梯，简单的解法都是递归，直接把公式敲一遍就好了，但是这里面会有很多重复的调用，改用迭代就会将时间从极大降低

LCS：这个的话，最简单的解法也是递归(如下)，从后向前拆分：

lcs(char* str1,char* str2){
    int len1 = strlen(str1);
    int len2 = strlen(str2);
    //递归基
    if(str1[len1-1] == str2[len2-1])    
        return str1[len1-1];
    return lcs(str1[0:len1-2],str2[0:len2-1]) + lcs(str1[0:len1-1],str2[0:len2-2])
}

但是这样效率极低，可以使用矩阵来存储结果，使用迭代来解决问题

lcs(char* str1,char* str2){
    int len1 = strlen(str1);
    int len2 = strlen(str2);
    //申请空间并初始化为0
    int* mutex = (int*)calloc((len1+1)*(len2+1),sizeof(int));
    //开始计算
    for(int i = 1;i <= len1;i++)
        for(int j = 1;j <= len2;j++){
            if(str1[i-1] == str2[j-1])
                mutex[i][j] = mutex[i-1][j-1]+1;
            else
                mutex[i][j] = mutex[i-1][j] > mutex[i][j-1] ? mutex[i-1][j] : mutex[i][j-1];
        }
}

向量

作为一种抽象数据类型，需要提供以下接口：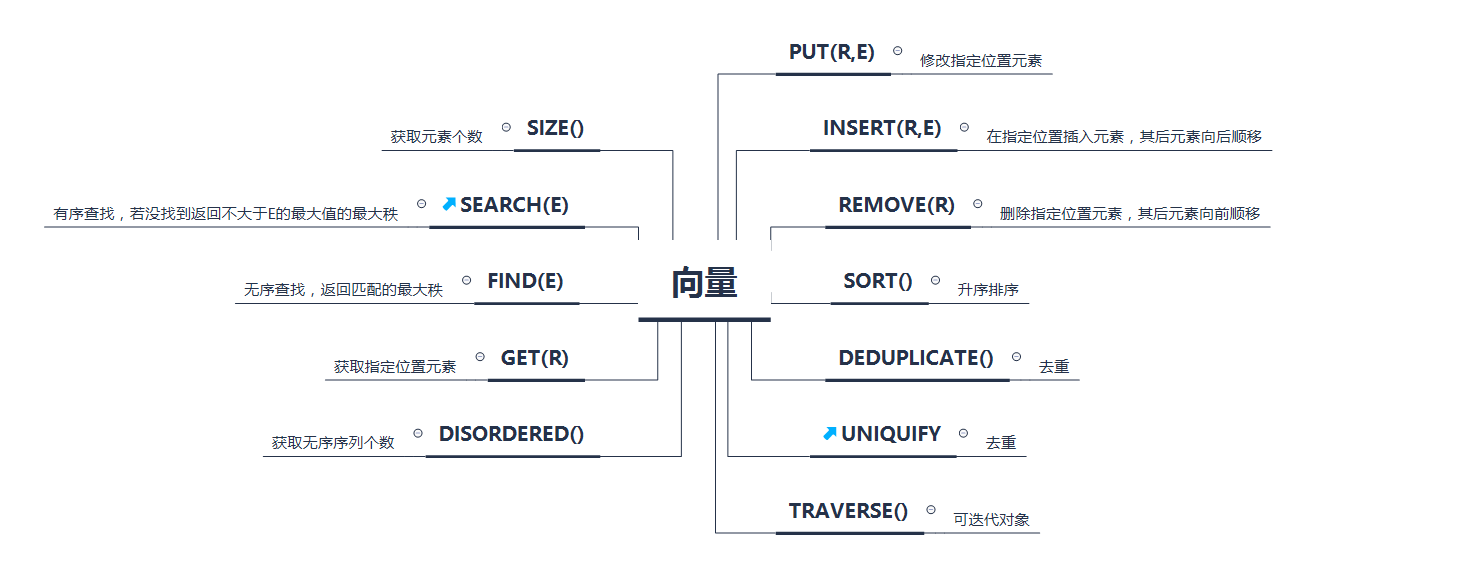

无序向量

唯一化

思路就是从第一个开始，向后遍历，判断每一个元素是否在之前出现过，有的话就删除当前元素：

deduplicate() {
	 int oldSize = _size;
	 Rank i = 1;
	 while (i < _size)
		 (find(_elem[i], 0, i) < 0) ? i++ : remove(i);
	 return oldSize - _size;
}

优化：

先排序再删除
先标记再删除

有序向量

唯一化

最简单的方式就是向后遍历，若相邻元素相等就删除后者，明显的他是正确的但是也是低效的。
稍微改进一下，就是从后向前遍历，明显的，这样的remove操作会更快。
仔细分析，它们两者的区别是，前者会对之后要删除的操作也进行若干次前移操作，这是不必要的，那再考虑后者，其实它里面的有效元素会进行多次步长为一的前移，这也是很浪费的，若是能一步到位效率会有很大提升。
定义两个指针，指针1指向前一组相同元素的第一个，指针2开始向后遍历找到下一组相同的元素，指向第一个，此时将指向的值放在指针1指向位置，指针1向后移，指针2继续之前操作。
1
2
3
4
5
6
7
8
9
10
uniquify() {
Rank i = 0，j = 0;
while(++j<_size)
if (_elem[j] != _elem[i]) {
_elem[++i] = _elem[j];
}
_size = ++i;
shrink();
return j - i;
}

查找

二分查找

O(1.5logn)

 binSearch(T* A,T const& e,Rank lo,Rank hi) {//左闭右开
	 while (lo < hi) {
		 Rank mi = (lo + hi) >> 1;
		 if (e < A[mi])hi = mi;
		 else if (A[mi] < e)lo = mi + 1;
		 else return mi;
	 }
	 return -1;
}

斐波那契查找

因为仔细观察上面查找，会发现看似平衡内部并不是真的平衡，左边只需要比较一次，右边需要比较两次，这样越深差距越大啦。为了实现真正的平衡，可以使用斐波那契数，若size的大小刚好等于fib(n)-1那么可以分为fib(n-1)-1，fib(n-2)-1,x这个三段长，这样整体的平均查找就会最均匀。

 fibSearch(T* A,T const& e,Rank lo,Rank hi) {
	 Fib fib(hi - lo);//初始化一个fib数列
	 while (lo < hi) {
		while (hi - lo < fib.get()) fib.prev();//获取到小于fib(hi-lo)的那一项的fib
		Rank mi = lo + fib.get()-1;//"中点"
		if (e < A[mi])hi = mi;
		else if (A[mi] < e)lo = mi + 1;
		else return mi;
	 }
	 return -1;
}

这里总体和二分查找类似，只是”中点”的选择上有所不同。所以这里的关键在于”中心”点的选取上，对于二分查找，选的是0.5这个中间点，而fib查找选择的是0.618这个黄金分割点比。于是可以猜测这个点的选择决定者这个算法的效率，若是猜测正确那么或许能够使用其他的比例来再次提高效率，于是设这个比例为λ，通过公式可以得出fib的确优于前一个二分查找。

改进的二分查找

fib是对原始二分查找的改进，他的思路是左右两边比较次数不等，那么比较少的那边就深一点，比较多的那边浅一点，最终两边比较平均，而另一种改进就是针对两边比较次数不同作出的，即使两边尽量相同：

binSearch(T* A, T const& e, Rank lo, Rank hi) {
 while (1 < hi - lo) {
	 Rank mi = (lo + hi) >> 1;
	 (e < A[mi]) ? hi = mi : lo = mi;       //这里他们是封闭的
 }
 return (e == A[lo]) ? lo : -1;
}

此时，将原来的三分支改为了现在的两分指，原来的中点合并到了右边，既然只有两个分支当然只需要一次比较了，这样就不存在向左向右比较次数不同的问题了。再来回顾一下之前定义接口的方法时，说的是当search未找到时，返回的不大于的值最大且秩最大的那个元素的秩，上面的都没有做到，于是再次修改：

binSearch(T* A, T const& e, Rank lo, Rank hi) {
 while (lo < hi) {
	 Rank mi = (lo + hi) >> 1;
	 e < A[mi] ? hi = mi : lo = mi + 1;
 }
 return lo--;
}

此时，中间的那个值又没有被包含在内了，但是却是正确了的，喵呀，喵不可言呀~=！

插值查找

之前的查找都没考虑数据内部的特点，但若是数据分布比较线性均匀且独立则可以使用另外一种较为快速的查找方法，它和上面差不多只是分段依据不同，根据：$\frac{mi - lo}{hi-lo} = \frac{e-A[lo]}{A[hi]-A[lo]}$得到mi，此时在数据量极大时，它可以快速缩小查找范围，它的复杂度为O(loglogn)，当然这种算法用起来限制是更多的，而且在数据量小时并不能很好的体现有点甚至效果更差，于是一般来说是首先通过插值查找，将查找的范围缩小到一定范围再使用二分查找。

排序

起泡排序

思路为若相邻元素逆序则交换，依次遍历扫描交换，直到不存在逆序为止：

void bubblesort(int A[], int total) {
    while(--total)
		for(int i = 0;i<total;i++)
			if (A[i] > A[i+1]) {
				swap(A[i], A[i+1]);
			}
}

此时$O(n^2)$，即使本来就是有序的也需要这么多时间，为了改进，观察发现当依次扫描没有发生交换就证明已经有序了，此时就可以结束扫描了：

void bubblesort(int A[], int total) {
	for(bool sorted = false;sorted = !sorted;total--)
		for(int i = 0;i<total-1;i++)
			if (A[i] > A[i+1]) {
				swap(A[i], A[i+1]);
				sorted = false;
			}
}

再次考虑，若整个序列后面不本来有序了，只有前面部分是无序的且无序部分的最大值也不大于有序部分，那么就能提早结束对有序部分的扫描，而怎么识别这一点，是通过记录每一次交换最后发生的位置来判断的，即在一次扫描中，最后一次交换后的位置是有序的，于是可以写出下面代码：

void bubblesort(int A[], int total) {
    last = total - 1;
    while(0 < last)
        prelast = last;
        last = 0;                       //每次将其初始为0
		for(int i = 0;i < prelast;i++)
			if (A[i] > A[i+1]) {
				swap(A[i], A[i+1]);
				last = i;               //记录交换的第一个元素，在最后后者就是最大的了，不需要再次交换
			}
}

归并排序

基于比较的算法，bubllesort复杂度存在上界$O(n^2)$与下界$O(nlogn)$，它是由输入决定的，而归并排序能够在最坏的情况下也为$O(nlogn)$，它的步骤如下：

将序列分为两个子序列 $O(1)$
对其归并排序 $2*T(\frac{n}{2})$
对子序列进行合并 $O(n)$

mergeSort(Rank lo,Rank hi){
    if(hi - lo <2 ) return ;
    int mi = (lo + hi) >>1;
    mergeSort(lo,mi);
    mergeSort(mi,hi);
    merge(lo,mi,hi);
}
merge(Rank lo,Rank mi,Rank hi){
    T* A = _elem + lo;
    int lb = mi - lo;T* B = new T[lb];
    for(Rank i = 0;i <lb; B[i] = A[i++]);       //将A前一半备份到B
    int lc = hi - mi;T* c = _elem + mi;
    for(Rank i = 0,j = 0,k = 0;j<lb||k<lc;){
        if((j<lb)&&(lc<=k||(B[j]<=C[k])))A[i++] = B[j++];
        if((k<lc)&&(lb<=j||(C[k]<=B[j])))A[i++] = C[k++];
    }
}

这里也很巧妙的节省了空间，C是A的后半段，但是不需要将C的元素备份出去，因为C是有序的，不会存在C之前的元素还未使用就被覆盖的情况。另外，再观察发现B与C的不对等导致若B提前结束那么C的移动操作是没有任何作用的，所以可以再对归并部分优化：

merge(Rank lo,Rank mi,Rank hi){
    T* A = _elem + lo;
    int lb = mi - lo;T* B = new T[lb];
    for(Rank i = 0;i <lb; B[i] = A[i++]);     
    int lc = hi - mi;T* c = _elem + mi;
    for(Rank i = 0,j = 0,k = 0;j<lb;){              //只有在B未移完时进行移动
        if((lc <= k)||(B[j] <= C[k]))  A[i++] = B[j++];
        if((k < lc)&&(C[k] < B[j]))    A[i++] = C[k++];
    }
}

列表

与向量不同，列表虽然在逻辑上是线性的但是实现上是使用链表，即空间上并不连续，这样的好处是修改容易，坏处就是读取耗时。

排序

选择排序

再次回顾bublleSort，在最原始的版本中，每一次会把当前工作域的最大元素放在最后一个位置，但是它放的方式是相邻交换这样一步一步向后移动，更好的方法是扫描时并先记录最大的，扫描结束再直接移动：

selectionSort(Posi(T) p,int n){
	Posi(T) head = p->pred;Posi(T) tail = p;
	for(int i = 0;i < n;i++)tail = tail->succ;
	while(1 < n){
		insertBefore(tail,remove(selectMax(head->succ,n)));//优化，直接改指针
		tail = tail->pred;n--;
	}
}
selectMax(Posi(T) p,int n){
	Posi(T) max = p;
	for(Posi(T) cur = p;1 < n;n--){
		if(!lt((cur = cur->succ)->data,max->data))
		max = cur;
	}
	return max;
}

插入排序

在选择排序中，无序部分最大值不大于有序部分最小值，而插入排序就无此限制，而且插入排序是输入敏感的呢！

insertionSort(Posi(T) p,int n){
	for(int r = 0;r < n;r++){
		insertAfter(search(p->data,r,p),p-data);
		p = p->succ;remove(p->pred);			
	}
}

然后捏，复杂度：最好时是$O(n)$最坏时是$O(n^2)$

#define swap(a,b) a^=b;b^=a;a^=b

void selectionSort(int A[], int total) {
//	int sorted = 0;
//	for (int i = 0; (i < total - 1)&&(sorted=!sorted); i++)
	for (int i = 0; i < total - 1 ; i++)
		for (int j = i + 1; j < total; j++)
			if (A[i] > A[j]) {
				swap(A[i], A[j]);
//				sorted = 0;
			}
}

栈

栈即向量列表的受限表示，它只能从一端存取元素，中间或者底部是不可见的，现在

进制转换

使用短除法可以将大的转换为小的，即反复除最后倒序输出余数，既然是倒序输出那么只有得到最后一个余数时才能开始输出，之前的结果必须被保存下来，那么保存余数需要的空间是不定的，可以使用对数算出动态申请一篇连续的区域或者直接用链表来实现，但是最后的操作总不那么直观，若使用栈就能很好的解决这个问题了，即输出次序与处理过程颠倒，递归深度和输出长度不易预知的计算可以使用栈解决：

convert(int n,int i){
	Stack result = new Stack();
	while(n){
		result.push(n%i);
		n = n/i;
	}
	while(!result.empty()){
		printf("%d",result.pop());
	}
}

括号匹配

括号匹配即输入一个表达式，判断表达式中括号是否匹配，匹配的依据是左括号对应位置一定有且是对应的右括号，解决问题有两种思路：由外向内与由内向外，明显的，前者虽然能够解决问题但是实现起来比后者更复杂，而后者使用栈能够很简洁的解决问题，即具有自相似性的问题可递归描述，但分支位置和嵌套深度不固定：

bool match(char* A,n){
	Stack s = new Stack();
	for(int i = 0; i < n;i++){
		switch(A[i]):
			case '(': s.push(')');break;
			case '{': s.push('}');break;
			case '[': s.push(']');break;
			case ')': 
			case ']':
			case '}': if(s.empty()||s.pop() != A[i])return false;
			default: ;
	}
	if(s.empty())return true;
	else return false;
}

栈混洗

将栈A中的所有元素通过某种方式使用中转栈转移到另一个空栈B中，这样同一个栈可能得到不同的栈混洗，因为栈A中剩余的元素的栈混洗与栈B中已有的栈混洗之间相互独立，那么它能得到的结果序列共有$\sum_{k=1}^n SP(k-1)*SP(n-k)$且$SP(1)=1$，则总数即为catalan数：$\frac{(2n)!}{(n+1)!n!}$，任意三个相邻元素1 2 3的栈混洗不可能是3 1 2，其他元素不会影响这三个元素的栈混洗序列，于是，为了甄别一个序列是否是另一个序列栈混洗，可以采用模拟栈混洗的方法，每次pop之前检查是否为空，pop之后检查是否与栈B相匹配。

中缀表达式求值

这可以说很像编译原理里面敲得代码了，给定表达式求值：

const char pri[N_OPTR][N_OPTR] = {
	//优先级表
}
char orderBetween(char a,char b){
	return pri[char2num(a)][char2num(b)];
}
evaluate(char* S,char* &RPN){
	Stack<float> opnd;Stack<char> optr;			//定义两个栈分别用于存放数据与运算符
	optr.push('\0');							//才开始向运算符栈压入0再配合字符串的0刚好组成一对括号
												//用于判断计算是否结束
	while(!optr.empty()){						//当还存在运算符说明未运算结束
		if(isdigit(*S)){
			readNumber(S,opnd);					//遇到数字直接入栈，注意这里S还应该移动
		else
			switch(orderBetween(optr.top(),*S)){
				case '<': optr.push(*S);break;	//当下一个优先级更高就压入下一个
				case '>': {
					cahr op = optr.pop();		//当下一个优先级更低说明该开始运算了
					if('!' == op)opnd.push(calcu(op,opnd.pop()));
					else
					{
						float opn2 = opnd.pop();
						float opn1 = opnd.pop();
						opnd.push(calcu(opn1,op,opn2));
					}
				case '=': optr.pop();S++;break;
				default: ;//出错操作
			}
		}
	}
	return opnd.pop();
}

逆波兰表达式

上面那种对于我们来说很直观的表达式计算机处理器起来是比较麻烦的(如上)，而逆波兰表达式(RPN)就会好处理很多，下面是个例子：

0 ! 1 + 2 3 ! 4 - 5 ^ - 67 * - 8 - 9 +

运算方式是遇到数字入栈，遇到运算符取出操作数，弹出的数据由右向左排序：

((!0 + 1) - ((2 - (!3 - 4)^5) * 67)) - 8 + 9

对于经常需要用到的表达式，转化为RPN表达式后运算效率会提高很多，而这里要学的就是转换方法：

手工方法：用括号显式指明所有运算符优先级，再将运算符移到对应右括号后，删除所有括号即可。

代码实现：观察手动实现的原理就是找到局部优先级最高的部分，将运算符一道后面，所谓局部优先级最高就是可以执行运算，前面的优先级大于后面，这和上面的中缀表达式求值本质上一样：

evaluate(char* S,char* &RPN){
	Stack<float> opnd;Stack<char> optr;			
	optr.push('\0');							
	while(!optr.empty()){						
		if(isdigit(*S)){
			readNumber(S,opnd);					
			append(RPN,opnd.top());										//遇到操作数直接放入尾部
		}else
			switch(orderBetween(optr.top(),*S)){
				case '<': optr.push(*S);break;	
				case '>': {
					cahr op = optr.pop();		
					append(RPN,op);										//当遇到当前优先级大于下一个优先级时说明该执行操作了，而这时就把这个运算符添加到尾部
					if('!' == op)opnd.push(calcu(op,opnd.pop()));
					else
					{
						float opn2 = opnd.pop();
						float opn1 = opnd.pop();
						opnd.push(calcu(opn1,op,opn2));
					}
				case '=': optr.pop();S++;break;
				default: ;
			}
		}
	}
	return opnd.pop();
}

队列

和栈一样，也是受限的序列，它只能操作首尾，尾入首出。并没什么特别的，简单的继承list就可以实现了。

词典

emmmm，学的时候好像是hash查找？不管啦，就当做词典吧。对于可用的空间很大但是实际用到的空间很小的情况，如电话本，将数据用链表组织能节省大量空间，但是查找时时间复杂度为$O(n)$，若使用数组实现寻下标访问时间复杂度为$O(1)$，但是将会需要$O(b^m)$个空间，而实际用到的空间远没这么多造成极大的浪费，另外，如文件这种东西他需要的空间是无限大的，将不可能实现，为了实现对这种情况的快速查找就有了词典这种东东，它就是将输入进行一些变换，称为数组的下标这样进行寻下标(秩)访问，变换的函数称为散列函数，它需要满足”确定”,”快速”,”满射”,”均匀”四个特性，先来记录一些比较简单的散列函数

散列函数

hash(key) = key % M M应为素数
hash(key) = (key + b)<<c % M M应为素数

冲突解决

树

向量适合读取，列表适合写入，而树糅合了这两个优点。

基本概念

树是一种特殊的图：T = (V , E) ，n = |V| , e = |E|
度：节点r孩子节点的数目称为其度：degree(r)
路径：根节点到节点v之间，用path(v)表示
深度：节点v到根节点路径长度为深度：depth(v)
高度：节点r到最低后代处的路径长度：height(v)定义空树的高度为-1
路径长度：路径上边的数目

实现方式

如下，这种矩阵空间利用率很高而且向上查找很快，但是若向下或者查找兄弟节点就需要遍历整个节点了：
如下，这种操作向下找孩子和平行找兄弟很快，但是向上找父亲又需要遍历，而且其实有一半的节点都没有孩子节点，还有的节点有很多孩子：
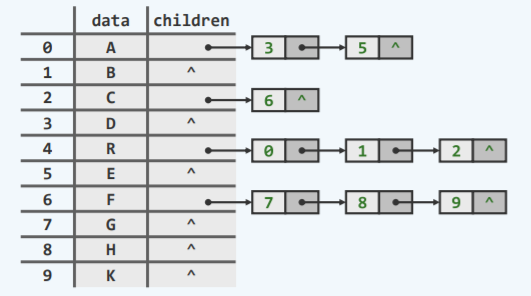
如下，只记录第一个孩子节点与第一个兄弟节点(一般,最右侧兄弟可以记录父亲节点)，每个方向都能在较快较稳定的时间内找到：

二叉树

基本概念

深度为k的节点至多$2^k$个。
真二叉树：每个节点度数为偶数。

二叉树转换

普通的树转换为二叉树，只需要使用长子兄弟表示法即可，此时原来的长子称为左孩子，而第一个兄弟成为右孩子。
反过来，二叉树从下到上，右孩子向上移到平级，直到遇到左孩子此时父亲节点连接所有孩子，就能还原为之前的树了。

遍历

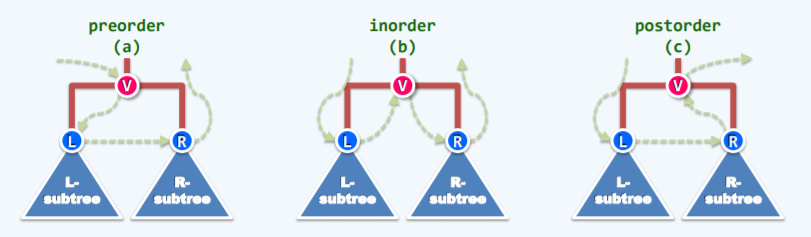
所谓先、中、后序，是指在有左右子树时，访问当前节点的顺序，任何一颗二叉树可以分为当前节点，左子树与右子树，最终目标是访问节点(说法不严谨)：

先序遍历：先访问当前节点，再递归遍历左子树到最底层，在左子树里面依然先访问当前节点，遍历完以后递归遍历右子树。
1
2
3
4
5
6
traverse(BinNodePosi(T) x,VST &visit){
if(!x)return;
visit(x->data);
traverse(x->lChild,visit);
traverse(x->rChild,visit);
}

中序遍历：先递归遍历左子树到最底层，访问左叶子节点后访问父亲节点再访问右叶子节点。

traverse(BinNodePosi(T) x,VST &visit){
    if(!x)return;
    traverse(x->lChild,visit);
    visit(x->data);
    traverse(x->rChild,visit);
}

后序遍历：先访问有叶子再访问左叶子接着再访问父亲。

traverse(BinNodePosi(T) x,VST &visit){
    if(!x)return;
    traverse(x->lChild,visit);
    traverse(x->rChild,visit);
    visit(x->data);
}

层次遍历：一层一层遍历。

travLevel(VST& visit){
    Queue<BinNodePosi(T)> Q;
    Q.enqueue(this);                          //先将自己入队
    while(!Q.empty()){
        BinNodePosi(T) x = Q.dequeue();
        visit(x->data);                       //访问取出队首
        if(hasRChild(*x))Q.enqueue(x->rChild);//将左右孩子添加到队列
        if(hasLChild(*x))Q.enqueue(x->lChild);
    }
}

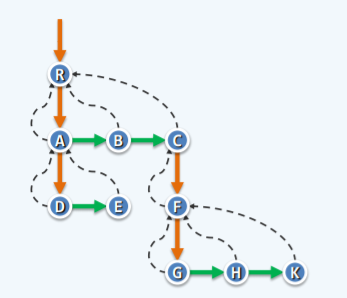
优化

对于先序遍历，观察递归调用的过程，最后面的调用最先返回，于是使用栈消除尾递归,手动实现递归执行顺序：

traverse(BinNodePosi(T) x,VST &visit){
    Stack<BinNodePosi(T)> S;
    if(x) S.push(x);                    //若传入的不是一个空节点就将其压入栈中
    while(!S.empty()){
        x = S.pop();                    //先访问此节点
        visit(x->data);
        if(hasRChild(*x))S.push(x->rChild);//将右孩子压入栈
        if(hasLChild(*x))S.push(x->lChild);//这样就可以像深度优先一样访问
    }
}

另外的，从宏观上观察可以发现它是先沿着左子树遍历完再倒着遍历右子树，对于右子树依然这样做，于是可以写出下面的代码(其实就是一个深度优先搜索)：

static void visitAlongLeftBranch(BinNodePosi(T) x,VST& visit,Stack<BinNodePosi(T)> &S){
    while(x){
        visit(x->data);
        S.push(x->rChild);      //这里可以加判断确定是否要入栈，没有也无所谓
        x=x->lChild;
    }
}
traverse(BinNodePosi(T) x,VST &visit){
    Stack<BinNodePosi(T)> S;
    while(true){
        visitAlongLeftBranch(x,visit,S);
        if(S.empty())break;
        x = S.pop();
    }
}

对于中序遍历，不是尾递归了，但是观察依然发现它先沿着左子树到最底部，然后访问左子树后对右子树进行相同的操作：

static void goAlongLeftBranch(BinNodePosi(T) x,Stack<BinNodePosi(T)> &S){  
    while(x){
        S.push(x);
        x=x->lChild;
    }
}
traverse(BinNodePosi(T) x,VST &visit){
    Stack<BinNodePosi(T)> S;
    while(true){
        goAlongLeftBranch(x,S);         //先沿着左子树到叶子节点
        if(S.empty())break; 
        x = S.pop();                    //然后取出叶子节点去访问
        visit(x->data);
        x = x->rChild;                  //访问以后就开始遍历右子树
    }
}

重构

将遍历序列重新恢复为原来的树，中序可以将一个序列分为左右子树，先序或后续能够识别父亲节点，即中序的中点节点，这样有了先序或者后序，再加上一个中序序列就能重构一颗二叉树啦。

图

概念

G = (V ; E) V代表顶点集，E代表边集合
关系：顶点与顶点之间存在邻接关系，顶点与边之间存在关联关系
路径：简单路径不含有重复节点
环路：路径的起点与终点重复
欧拉环路：经过所有边一次且恰好一次的环路
哈密尔顿环路：经过每一个顶点一次

邻接矩阵

它为n行n列(n=|V|)，表示两个点之间是否存在邻接关系或者权重。那么它的大小为$n^2$，但一般来说$e<<n^2$，一个普遍的情况，一个平面图$e<=3*n-6$，即空间利用率约为$\frac{1}{n}$。

注 关联矩阵：即存储顶点与边关联关系的矩阵，它有n行e列（e=|E|）

广度优先搜索

耗空间省时间的遍历，使用队列实现，代码如下：

BFS(int v,int& clock){
    Queue<int> Q;
    status(v) = DISCOVERED;
    Q.enqueue(v);
    while(!Q.empty()){
        int v = Q.dequeue();
        dTime(v) = ++clock;
        for(int u = firstNbr(v);-1 < u;u = nextNbr(v,u))

        status = VISITED;
    }
}

深度优先搜索

来源参考

[1]清华大学-邓俊辉-《数据结构》